Neural Networks are the foundation of Deep Learning. Any problem that cannot be solved using traditional machine learning algorithms might be solved using neural networks. Generally, the neural networks are implemented using the libraries and modules like TensorFlow, Pytorch, and many more libraries. The neural network’s actual architecture remains unknown as the libraries used by the programmers just act as a black box. The data is made compatible with the neural network’s (black box’s) input layer, and the programmers get the output after processing takes place in the black box.
This article unveils the architecture of this black box and the fundamental algorithms of deep learning models. Implementing direct functions from the libraries limits the problem-solving approach; this article aims to explain the overall concept and logic behind building Neural Networks from scratch.
What are Artificial Neural Networks?
The biological neural networks form the foundation of the human nervous system, enabling the brain to learn. On a similar note, artificial neural networks try to perform the same functions. These functions include supervised learning, unsupervised learning, and reinforcement learning. We will not go in-depth with every learning type. Instead, we will focus on the artificial neural network that performs supervised learning. 
Supervised learning focuses on training the dataset containing input-output data points and it adjusts its weight according to the relationship between these data points. Since supervised learning uses this exact relation, hence it tends to be accurate and efficient in most problems and use cases. Although if target/output data is not available then supervised learning cannot be implemented. This is one of the major drawbacks of Supervised Learning. In this tutorial, we will work on the dataset which has both input and output/target data points. Thus supervised learning can be used on this type of dataset for training the neural network.
Dataset For Training and Testing the Neural Network
We will use the most straightforward dataset for a better understanding. Hence, we will be using the OR logic gate dataset. The OR logic gate is easier to understand as it has two inputs and one output. Also, the dataset will have only 4 data points as all the possible combinations for a two-input binary system will be 2^2=4.
OR Logic Gate Configuration
| Input 1 | Input 2 | Output |
| -1 | -1 | -1 |
| -1 | 1 | 1 |
| 1 | -1 | 1 |
| 1 | 1 | 1 |
Designing the Architecture of Neural Network
The OR logic gate dataset has two inputs, hence there will be two units in the input layer. Similarly, there will be one unit in the output layer. Conventionally a bias is also present in the input layer to monitor the thresholds during input variations. In this tutorial, we will not complicate things by adding a hidden layer as the objective is to understand the basic architecture of the neural network. Hence, only three weights are required for this type of network, 2 for the input inputs and 1 for the bias value.
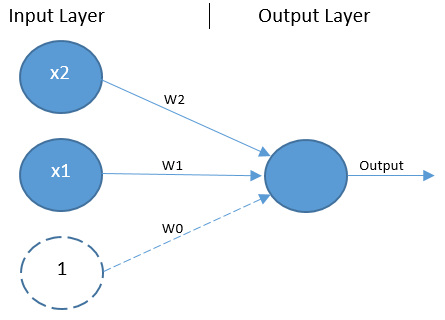To summarise the architecture, we have three layers in the neural network. These are:
- Input Layer: Two input units and a bias unit
- Weights: Three weights corresponding to each unit in the input layer
- Output Layer: One output unit
- Activation function
The activation function takes the aggregated value of the neural network as its input and gives the network’s overall output. In this tutorial, we will be using the bipolar binary activation function.
NOTE: For a robust dataset, we will have to use hidden layers as well.
Building the Neural Network using Python
Till now we have understood the concepts and dataset which we will be using. Let’s begin programming the neural network using Python. We assume you already have python setup on your IDE or code editor. We will be using VS Code IDE for this tutorial.
Importing Libraries and Defining Activation Function
We will just need two external libraries for this use case as we are building the simplest possible neural network. These libraries are numpy and pandas. We will be using numpy for numerical computations while training the network. Pandas library is for representing the outputs in the form of a data frame for better representation.
As we are using bipolar binary activation function, thus we need to define it before calling it in the main program. The bipolar binary activation function outputs +1 for all inputs greater than or equal to zero. Similarly, it outputs -1 for all inputs less than zero. Hence, we can build a simple if-else logic for implementing this. The code snippet for importing libraries and defining activation functions is given in the below image.
Initializing the Layers of the Neural Network
We saw two units in the input layer and a total of 4 combinations for the input data. Hence, we will create a nested list using the numpy array function. Use the ‘X’ variable for this nested list. You need to provide random values to the weights corresponding to the input units and the network’s bias. Use the ‘W’ variable for weights corresponding to input units and the ‘b’ variable for the weight corresponding to bias input. Now, create a 1-dimensional array for expected output/target values with the ‘T’ variable. Define a suitable learning rate for the network with the ‘a’ variable. The code snippet for initializing the layers of the neural network is given in the below image.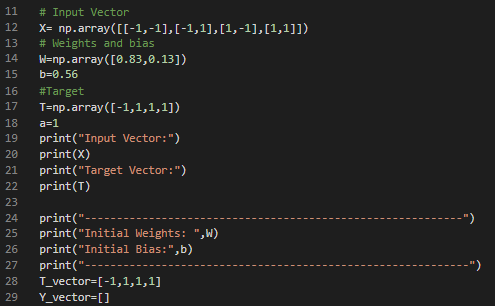
Iterative Supervised Learning for the Neural Network
The weights need to be adjusted according to the input-output values, thus it has to go through iterations for updating its values according to the relation between the input and target features. The weight updating algorithm for this neural network is similar to the perceptron learning rule.
- ΔW=α * input value * target value
- Δb= α * target value
- W= W+ ΔW
- b= b+ Δb
Where α is the learning rate for the network. Every iteration of all the input values is counted as one epoch of supervised learning. After every epoch, if the network’s target values and output values match with each other, then the iterative learning is stopped and the weights are finalized.
During every iteration, the input values are multiplied by the weights. These values are added to find an aggregation value that becomes the input for the activation function to obtain the final output values. These are the network’s actual output values that are checked with the target values after every epoch. The code snippet for iterative supervised learning is given in the below image.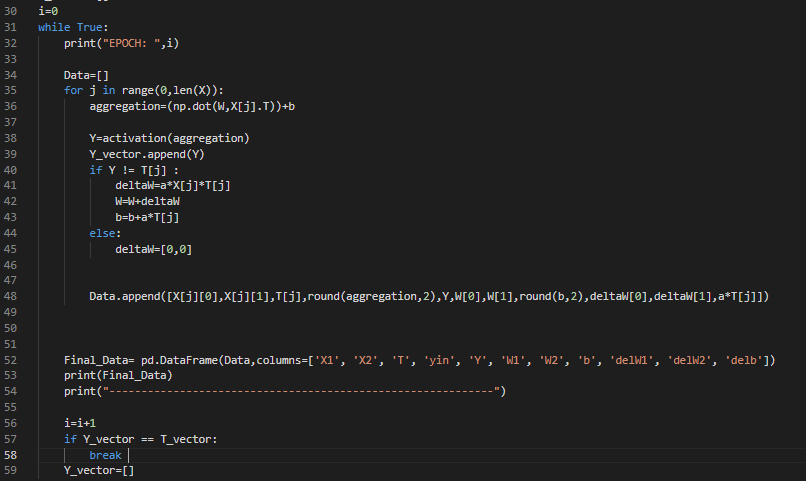
Final Output
Pandas library is used to represent all the values of each epoch in the form of a data frame so that the output is organized. There are 11 columns for this data frame ranging from all the input values, weights, target values, aggregation value, and delta values for the weights. The output image after running the code is as follows.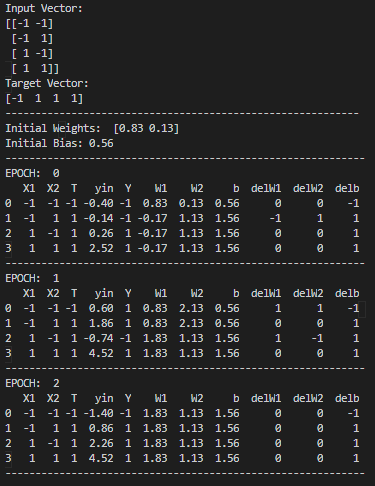
Python Code for Building Neural Network from Scratch
import numpy as np
import pandas as pd
def activation(z):
if z>=0:
Y=1
else:
Y=-1
return Y
# Input Vector
X= np.array([[-1,-1],[-1,1],[1,-1],[1,1]])
# Weights and bias
W=np.array([0.83,0.13])
b=0.56
#Target
T=np.array([-1,1,1,1])
a=1
print("Input Vector:")
print(X)
print("Target Vector:")
print(T)
print("-----------------------------------------------------------")
print("Initial Weights: ",W)
print("Initial Bias:",b)
print("------------------------------------------------------------")
T_vector=[-1,1,1,1]
Y_vector=[]
i=0
while True:
print("EPOCH: ",i)
Data=[]
for j in range(0,len(X)):
aggregation=(np.dot(W,X[j].T))+b
Y=activation(aggregation)
Y_vector.append(Y)
if Y != T[j] :
deltaW=a*X[j]*T[j]
W=W+deltaW
b=b+a*T[j]
else:
deltaW=[0,0]
Data.append([X[j][0],X[j][1],T[j],round(aggregation,2),Y,W[0],W[1],round(b,2),deltaW[0],deltaW[1],a*T[j]])
Final_Data= pd.DataFrame(Data,columns=['X1', 'X2', 'T', 'yin', 'Y', 'W1', 'W2', 'b', 'delW1', 'delW2', 'delb'])
print(Final_Data)
print("------------------------------------------------------------")
i=i+1
if Y_vector == T_vector:
break
Y_vector=[]
