Machine learning is a branch of computing, which includes algorithms that learn by themselves. Learning by oneself, what does this mean? Quite simply, at the beginning, an automatic learning algorithm does not know how to do anything; then, as it trains on data, it is able to respond more and more effectively to the task it is asked to do. A bit like you and me, sort of. Today, we are going to talk about machine learning, especially the Support Vector Machines (SVM) family.
We can thus classify the algorithms into two categories:
1. “Classical” algorithms, where the algorithm simply applies a series of rules without learning from previous cases
2. The machine learning algorithms, where the algorithm is able to learn from the data already seen.
But above all, what is an SVM? Behind this barbarian name (which is the acronym for Support Vector Machines) is hidden an algorithm of automatic learning, and which is very effective in classification problems.
What is a Support Vector Machines?
First of all, let’s start by setting a framework for what we will see. In particular, what is a classification problem?
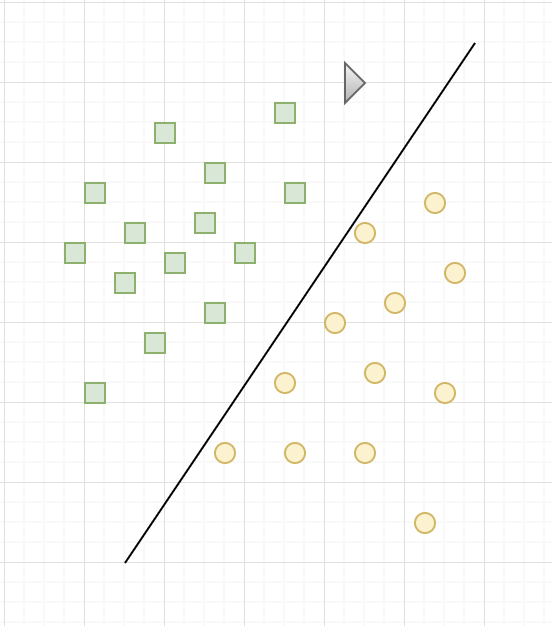
Consider the following example. We have a plane, and we have two categories: the yellow circles and the green squares, each occupying a different region of the plane. However, the border between these two regions is not known. What we want is that when we will present a new point, of which we only know the position in the plane, the classification algorithm will be able to predict if this new point is a yellow circle or a green square.
Here is our classification problem: for each new entry, determine to which category this entry belongs.
In other words, we must be able to find the boundary between the different categories. If you know the boundary, which side of the boundary belongs to which point, you can find the category to the new point belongs to.
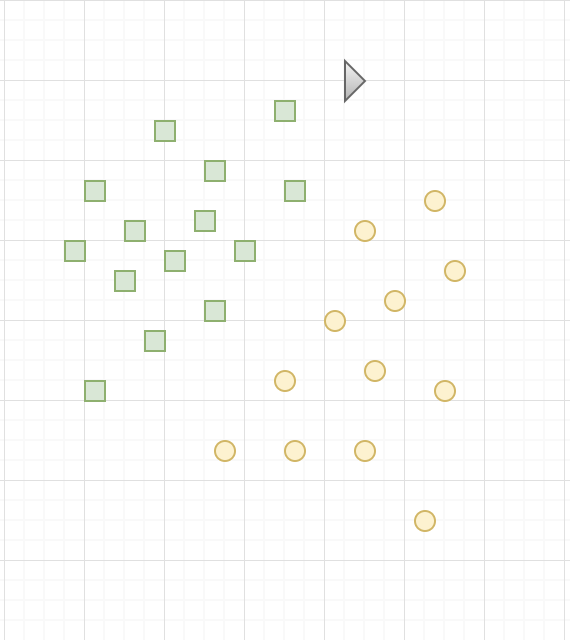
In order for the SVM to find this boundary, it is necessary to give it training data. In this case, the SVM is given a set of points, of which we already know if they are yellow circles or green squares, as shown above. From this data, the SVM will estimate the location of the hyperplane that is most plausible to the border.
Once the training phase has been completed, the SVM has found, from training data, the assumed location of the boundary. In a way, it “learned” the location of the border with the training data. What’s more, the SVM is now able to predict which category belongs to an entry that it had never seen before, and without human intervention (as is the case with the black triangle in the figure below), is the interest of machine learning.
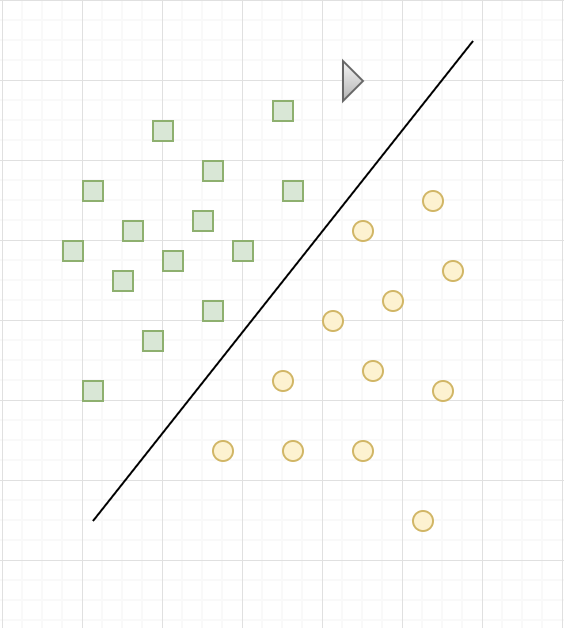
As you can see in the figure above, for our problem, the SVM chose a straight line as border. This is because, as has been said, the SVM is a linear classifier. Of course, the frontier found is not the only possible solution, and is probably not optimal either.
However, it is considered that, given a set of training data, the SVM are tools that get some of the best results. In fact, it has even been proven that in the class of linear classifiers, SVMs are the ones that get the best results.
One of the other advantages of SVMs, and it is important to note, is that they are very efficient when you only have a little training data; while other algorithms would not be able to generalize correctly, we observe that the SVM are much more efficient. However, when there are too many data points, the SVM tends to decrease in performance.
Now that we have defined our framework, we can go to the SVM. On the way!
How does a Support Vector Machine work?
Okay, so we know that the goal for an SVM is to learn how to place the boundary between two categories. But how to do it? When we have a set of training points, there are several straight lines that can separate our categories. Most of the time, there are infinite. So which one to choose?
Intuitively, we think that if we are given a new point, very close to yellow circles, then this point is likely to be a yellow round too. Conversely, the closer a point is to green squares, the more likely it is to be a green square. For this reason, an SVM will place the border as far as possible from the green squares, but also as far as possible from the yellow circles.
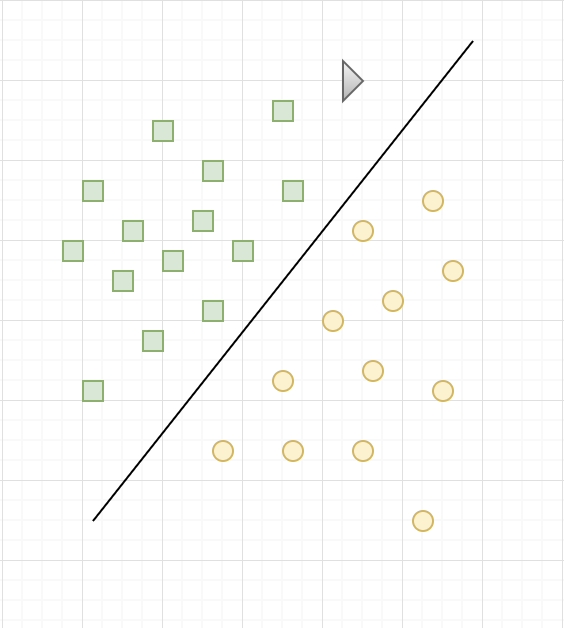
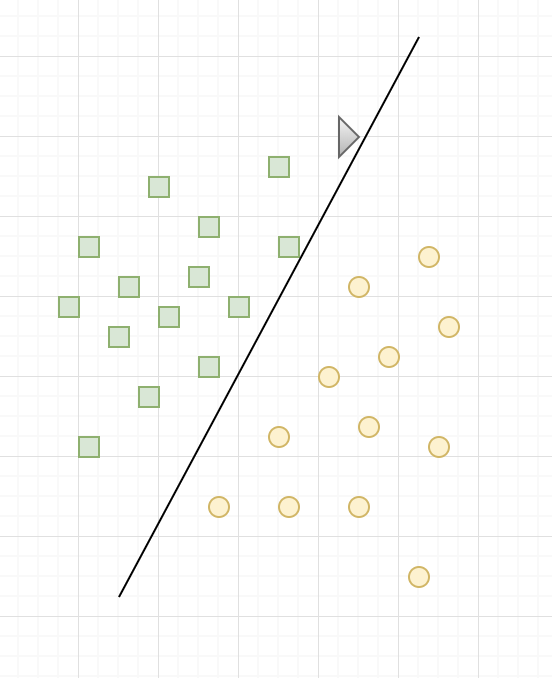
As seen in the figure above, it is the most remote frontier of all training points that is optimal, it is said that it has the best ability of generalization. Thus, the goal of an SVM is to find that optimal boundary, maximizing the distance between the training points and the boundary.
The training points closest to the border are called support vectors, and it is from them that the SVM gets its name. SVM stands for Support Vector Machine.
Linear SVM
Consider a dataset having n points represented as
![]()
where![]() is the normal vector to the hyperplane. The parameter
is the normal vector to the hyperplane. The parameter 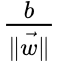 is the offset of the hyperplane from the origin along the normal vector
is the offset of the hyperplane from the origin along the normal vector![]()
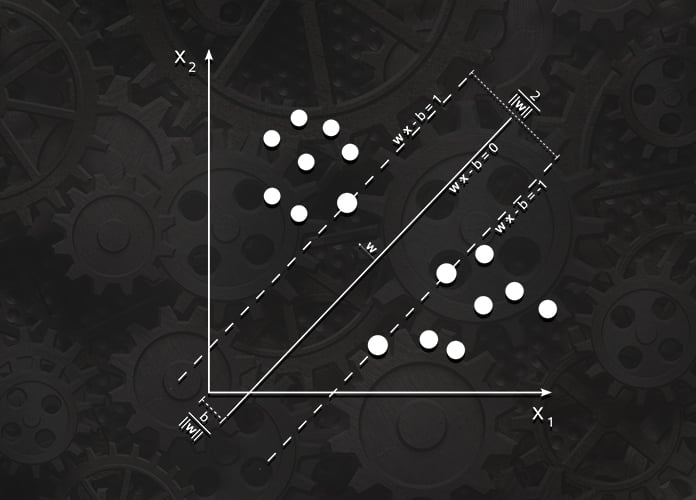
In case the training data is linearly separable, there can be 2 hyperplanes selected such that they separate the 2 classes of data and the distance between them is as large as possible. The “maximum margin hyperplane” lies halfway in between these 2 hyperplanes, and the region bounded by these 2 hyperplanes is known as “margin”.
If the dataset is normalized, the hyperplanes can be denoted as:
![]() (if the data points on or above it have class label as 1)
(if the data points on or above it have class label as 1)![]()
The distance between the above 2 hyperplanes is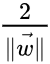 . Hence, if we want to maximize this distance, we will have to minimize
. Hence, if we want to maximize this distance, we will have to minimize![]()
The constraint stating that each data point must lie on the correct side of the respective hyperplane can be written as:
![]()
Hence, we can summarize all the constraints mentioned above into an optimization problem to find the maximum margin hyperplane:
Minimize![]() subject to the condition
subject to the condition ![]()
The maximum margin hyperplane is largely determined by the data points that are near to it, which are known as Support Vectors.
In this article, we have discussed about the Support Vector Machine. Hope you found it useful. Stay tuned for more articles!